Deals with concepts from Jacob’s Geometry Chapter 5. Learning about Pythagorean Theorem, and the extension to this theorem called Theorem 38 (Triangle Inequalities Theorem).
These two concepts can seem to be at odds with each other, but in this explanation we show you how this question can be tricky, but you have the knowledge to out smart it!
Check out the explanation below:
What you are learning about here is called ‘Theorem 38″ or “The Triangle Inequalities Theorem” (pg. 201)
What it is telling you is that the sum of two sides of a triangle have to be greater than the third side.
In number 97 in the Midterm Review of Geometry, they are asking a trick question.
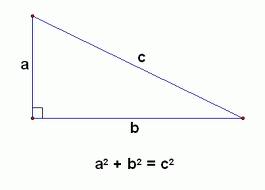
We know that the Pythagorean theorem says that
However, in this problem it specifically asks if we can have a triangle with side lengths a^2, b^2, and c^2, where the sum of a^2 and b^2 equals c^2. The answer is No. What?? Are we crazy?? Well, possibly, but that’s not the answer. 🙂 The distinction here is that the pythagorean theorem applies to side lengths, where “a” “b” and “c” represent the value, in length, of the side. If you take those lengths, and square them, then the relationship of a^2 + b^2 = c^2 makes sense.
What you have to be careful of, though, is that the SIDE LENGTHS for this hypothetical triangle in number 97 is not asking about what happens when you square the side lengths, it is asking what happens if the side length already ARE a squared value, then can the triangle exist? And the answer is no. Because if we add a^2 and b^2, we get c^2 (per the pythagorean theorem) so those side lengths are not possible in a triangle.
You can test this theory by trying to create a triangle with side lengths a^2, b^2 and c^2. (remember that the side length has to be squared values, not distances that you later square on paper).
Let’s give it a try together. Here is an example that will help.
In this example problem they try out different side lengths and see if it is possible to form a triangle with them based on combining the simultaneous truths of the Pythagorean Theorem along side Theorem 38. I would encourage you to look specifically at the ones they say are “not possible” and try to draw them out on paper, using the measurements they indicate in the example. What happens? The ones that violate Theorem 38 are not possible to form.
Admittedly the question in the midterm review is tricky, but it was good hearted. They are trying to get you to think about what you’re doing when you evaluate the side lengths of a triangle and realize that these relationships work together in complicated ways worthy of close attention 🙂 I hope this helps you, but feel free to write again if we can help! (Oh, and there is a formulary in the back of the Geometry book that if you have not already found it might truly be helpful. They take all of the theorems and postulates and put them in one place. Starts on pg. 738. The glossary is cool too. )
Hope this helps!